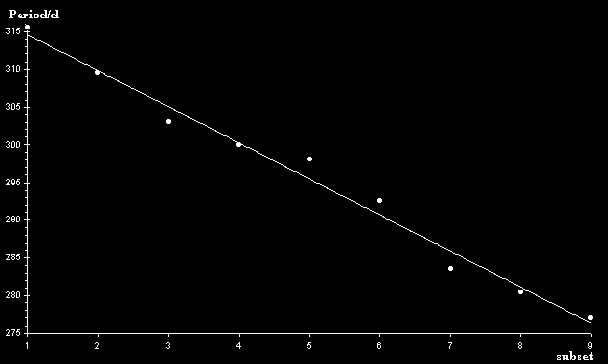
Average Periods per 12 cycles for R Aquilæ from Sep 1908 to Jan 1997. The “best fit” line has a slope of -4.8.
from VSSC94
Observations for R Aquilæ from September 1908 to January 1997, amounting to 109 cycles of this Mira variable, were taken from the full 1899 to 1997 BAAVSS archive and separated into 9 sequential groups of exactly 12 cycles each (with 13 cycles in one instance where a maximum had been completely missed due to seasonality). Unfortunately there was a complete gap in the archive for the years 1934 to 1938 inclusive which would have meant having to start the investigation from 1939. In order to avoid this problem, and further so as not to waste the excellent data between 1908 and 1934, this interregnum was filled via the AFOEV public domain archive at the CDS, Strasbourg1. An average period was derived for each of these cycle groups with software utilising the Phase Dispersion Method2 as shown in the following table:
| subset | Period(d) | DP(d) | datapoints |
|---|---|---|---|
| 1 | 315.5 | 1425 | |
| 2 | 309.5 | -6.0 | 1984 |
| 3 | 303.0 | -6.5 | 1598 |
| 4 | 300.0 | -3.0 | 863 |
| 5 | 298.0 | -2.0 | 854 |
| 6 | 292.5 | -5.5 | 739 |
| 7 | 283.5 | -9.0 | 1548 |
| 8 | 280.5 | -3.0 | 1856 |
| 9 | 277.0 | -3.5 | 1049 |
| mean -4.8 | |||
Giving a mean rate of 0.4 days change in period per cycle, which using a crude approximation [0.4 x ((13 x 365.25)/277)] leads to the prediction of an average period of around 270 days by the year 2010.
It should be noted, however, that not only is there a large scatter for the
period’s rate of decline between subsets, but also periods within each subset
also vary widely, sometimes markedly lengthening with respect to a previous
period. The decline is, therefore, not necessarily as smooth as first shown.
All the averages quoted had a statistical significance level2 of
better than 0.2 on an inverse scale ranging from 1.0 (essentially random) to
0.0 (infinitely accurate).

Average Periods per 12 cycles for R Aquilæ from Sep 1908 to Jan 1997.
The “best fit” line has a slope of -4.8.
The data was independently processed in order to generate an O-C diagram.
The zeroth maximum of JD 2418213 was defined as the base epoch and 315½, the
value derived from the first subset (above), was defined as the period. Then
“actual” times of maxima were laboriously derived for as many of the 109
cycles as possible (104 in total). A plot of the derived observed minus
calculated epochs was then plotted against cycle number as shown:
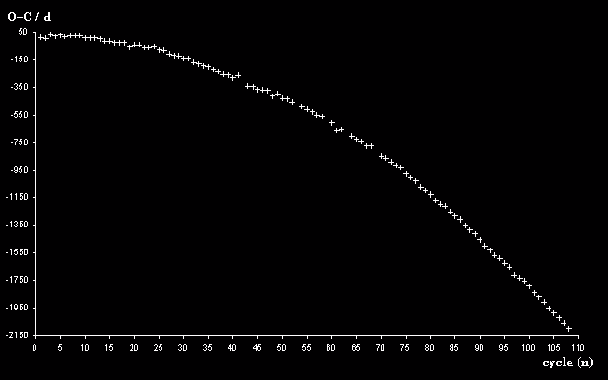
Observed - calculated epochs in days plotted against their cycle number, n.
Base epoch is JD 2418213, cycles are folded on a period of 315½ days.
The resultant curve is fitted by the quadratic function
y = -0.1871x2 + 0.5402x + 20.011.
Using this value for DP/P in the formula3
and noting that (O-C)n denotes the total discrepancy between the observed epoch and the epoch as calculated from the base epoch and period (and not the last known epoch of maxima and/or period) we can substitute within it to give the following predicted maxima:
| cycle | maximum | cycle | maximum |
|---|---|---|---|
| 110 | 13/10/1997 | 119 | 06/07/2004 |
| 111 | 14/07/1998 | 120 | 04/04/2005 |
| 112 | 15/04/1999 | 121 | 31/12/2005 |
| 113 | 13/01/2000 | 122 | 27/09/2006 |
| 114 | 13/10/2000 | 123 | 24/06/2007 |
| 115 | 13/07/2001 | 124 | 20/03/2008 |
| 116 | 12/04/2002 | 125 | 15/12/2008 |
| 117 | 09/01/2003 | 126 | 10/09/2009 |
| 118 | 09/10/2003 | 127 | 05/06/2010 |
By simply subtracting the previous date from each of the current ones and assuming an (unreal) smooth decline in period, as these predictions suggest, we find that by 2010 the period has declined to around 269 days, not greatly dissimilar from the 270 days derived by the completely independent approach used above.
Finally, by folding the BAAVSS data for the last dozen complete periods
around their derived average period of 277 days we obtain the following phase
diagram, which is included both as a representative light curve and an
indication of the “goodness of fit” of the data (two complete cycles are
shown for illustrative purposes):
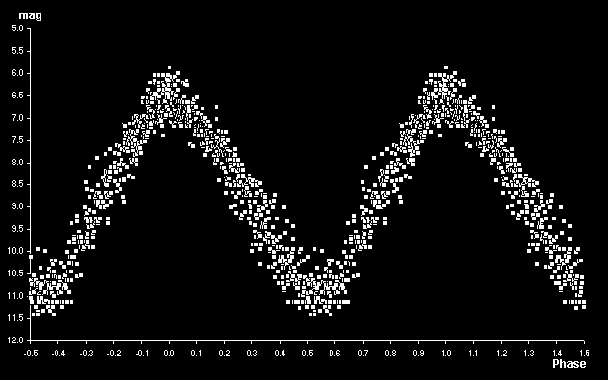
2 Written by Andreas Widjaja, Department of Astronomy, Faculty of Mathematics and Science, Bandung Institute of Technology (ITB), Jalan Ganesha 10, Bandung 40132, INDONESIA
3 Percy, John R (Ed). The Study of Variable Stars Using Small Telescopes, CUP 1986
Long-term light curve | observer list