Maxima of Chi Cygni

Dave McAdam

As noted in the BAA Journal1, chi Cygni was the first variable to exceed a 100 year record in the BAAVSS database. Now there are several more and although I am usually pre-occupied with the task of logging further observations old and new, it is difficult not to want to do at least some analysis on such a wealth of data. A program was written some time ago for compiling lists of mira maxima and minima directly from the archive and recently Karen Holland suggested short articles based on these lists could be considered for publication. Also, John Greaves has discussed in letters further statistical techniques which I might easily add. This encouragement has led me to check through the existing program and at the same time derive 91 maxima for chi Cygni. 86 minima were also derived in a similar way but only the maxima are discussed here.


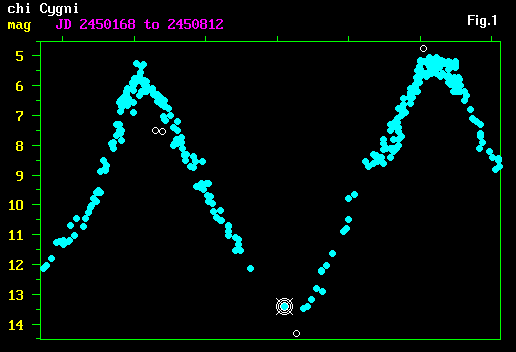
Maxima are determined by first loading two years of data into the program and selecting a suitable 'window' with a double edged curser set initially to 50 days width and then adjusted as necessary. Fig.1 shows the display of 1996 to 1997 before defining the window. Stray observations (shown as open circles) can be omitted from the calculation by stepping the crossed concentric-circle indicator along the observation set.

Least-squares quadratic equations2 are then applied to the selected set of observations and the JD at maximum of the fitted parabola (Fig.2) is filed along with the UT date, the days before and after maximum in the time window, the number of observations used and any excluded, the 'goodness of fit' and the magnitude.

The goodness of fit is simply estimated by eye as either Good, Average, or Poor. Some maxima only have 3 or 4 available estimates giving a very inaccurate determination of the magnitude. In such cases the magnitude is omitted from the file even though the time of maximum is retained. For other maxima only the rising or fading slopes are well observed and the centreline of the parabola is obviously too early or too late. In these difficult instances, an approximate JD can be entered as a last resort if it is felt of any value to do so. The fit is then listed as 'Estimated' without the other parameters. None of the chi Cyg maxima were estimated although several poor ones were listed. Fig.3 shows the fit to the second (1997) maximum from Fig.1. It is recognised that using a parabolic fit could produce a systematic error on miras with strongly asymmetric lightcurves. However, using a minimum practical time window excludes the flanks and produces good results for well observed maxima, Fig.2 & Fig.3 being typical.

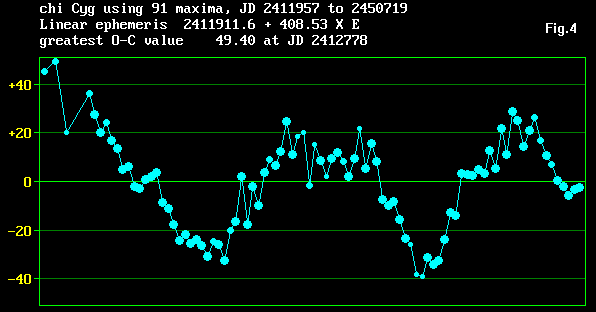
When the table of maxima is completed, a least-squares line is fitted to them (so called 'Linear Regression'3) thus deriving the elements from which a series of O-C values are generated. For this the program applies weights of 3, 2, and 1 for Good, Average, and Poor (or Estimated) maxima and Fig.4 indicates these with Large, medium, or small dots respectively. As can be seen, the O-C values range from -40 to +49 days with the latter occuring in the 1890's near the beginning of the dataset. Although the pre-1905 observations could not be checked and validated to the same extent as later results, the initial excursion of these early O-C away from the fitted (zero) line is probably real; we can see in other places that consecutive O-C (of Good fits) differ by up to plus or minus 20 days and conclude that times of maxima of chi Cyg really do wander by this amount. The rough sinusoidal shape of the O-C diagram indicates that a periodic term would tend to 'straighten it out', but I believe such terms are no longer thought to describe real cyclic phenomena in mira stars. 

Predicted maxima from the derived elements; 2411911.6 + 408.53E

    JD2451130 = 1998 Nov 12  (The 1998 BAA Handbook gives Nov 08)
    JD2451538 = 1999 Dec 25
    JD2451947 = 2001 Feb 06
    JD2452356 = 2002 Mar 22
    JD2452764 = 2003 May 04
References;
  1. D McAdam; letter BAAJ 107,6,1997 p302. A 100+year BAA record
  2. Jean Meeus; 'Astronomical Algorithms' Willman-Bell Inc. 1991 p43.
  3. ibid; p36.