From VSSC104

ST LMi: the first CCD photometry from Lymm

John Saxton

Introduction

Recently, I bought a Starlight-Xpress CCD camera, after more than a decade of doing photometry with a photomultiplier tube (PMT). PMT photometry can certainly produce accurate results, but is only suitable for use on bright objects, and requires practically perfect sky conditions, which are not common here in Cheshire. So I finally decided that the time had come to take the plunge and buy a more versatile detector. Karen Holland suggested that my initial experiences of using the camera for variable star work might make a suitable article for the VSSC. So here follows an account of the first CCD photometry at Lymm.

Linearity Testing

My camera is a Starlight Xpress MX916. I chose this camera since it has the largest chip area and largest full well capacity of the Starlight Xpress range. The former increases one's chances of getting suitable comparison stars in the same field as the variable; the latter helps to ensure a large dynamic range. One potential problem, however, is that the CCD chip used in the MX916 has anti-blooming gates. In some cases this has been known to render cameras non-linear and unsuitable for photometric work.

Therefore, before my camera arrived, I built a device to test its linearity. Briefly, this device consists of a light-tight metal can, containing a small white illuminated target, which is viewed by the CCD camera. The target is illuminated by a light-emitting diode (LED), which is pulsed once every four seconds by a special timing circuit which uses a quartz oscillator. The on time can be varied from 4 ms to 400 ms in steps of 4 ms. In operation, one starts an exposure of (say) 40 seconds, and immediately thereafter sets the pulse generator running. The CCD camera sees 10 pulses in this instance, and the total light in each pulse can be easily and accurately set from 1 to 100 units. Shortly after the camera arrived, Richard Miles, Andy Hollis and myself characterised its linearity. We quickly found the camera's response to be linear to 0.2% at up to 50 % of full scale (full well capacity), which seems entirely satisfactory for photometry, provided one stays in the lower half of the range.

Installing the camera on the telescope

My first CCD images were taken with the camera attached to my 8-inch guiding telescope, as the focussing mount had enough travel to allow me to focus the camera. In mid March, however, one of Norman Walker's filter boxes arrived on loan from the BAA. This has BVRI filters and an unfiltered position. The box measures approximately 6x6x3 inches. My main (8.5 inch) telescope has a square wooden tube, and the filter box is attached directly to the wooden tube. Norman supplied me with an adapter which is threaded to take the filter box, and also has countersunk holes for wood screws. The camera screws into the back of the filter box, and the whole assembly is very rigid (which is desirable, since the filter box is quite heavy). The next problem is focussing, which can now only be done by moving the primary mirror. (Before I started on this exercise, I had checked that focussing was theoretically achievable.) I had to move the mirror about 1 cm forwards in its cell, which was certainly not trivial, but after a few nights of fiddling I had achieved satisfactory focus and alignment with the colour filters in place. The focus has been left fixed since. Since the filter box has an unfiltered position, rather than a clear piece of glass, unfiltered observations are not possible with my system.

Observing

In late March, I had several successful nights observing. I obtained several images of M67 for calibration purposes, which are not yet fully reduced. I was particularly eager to do some time series photometry of a cataclysmic variable. But what star should I observe for my first attempt ? I wanted something with which to test my system, but I also wanted to be confident of getting at least some results. After perusing Brian Warner's book, I decided on the polar ST LMi. It is faint enough (V=14.7 to 17.2 according to his table 6.1) to be a fairly severe test of the system, but also has a large amplitude of variation, so that I would hopefully see something even if my signal to noise ratio turned out to be poor. The orbital period is short enough (114 minutes) for it to perform in a single observing session. As a bonus, polars like ST LMi also change colour throughout their orbital cycle, becoming redder at maximum light.

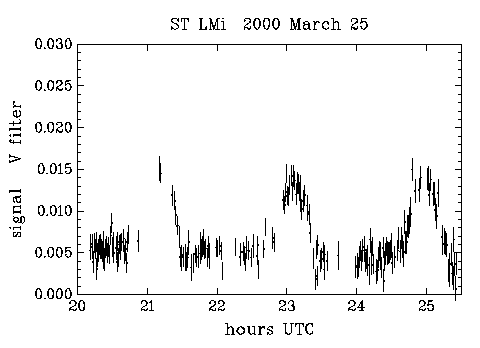
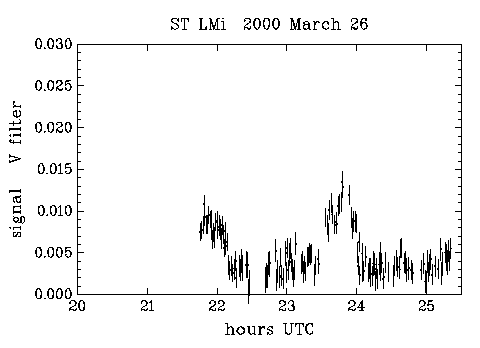
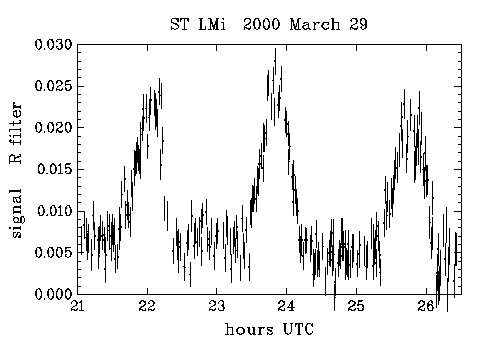
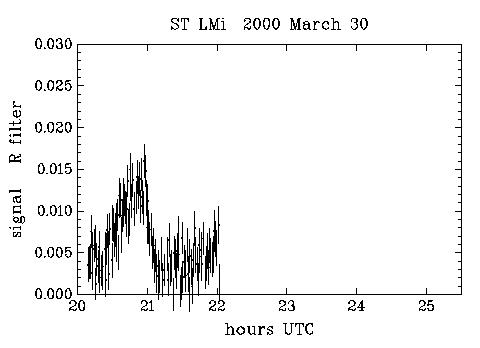
Between 25 March and 30 March, I obtained four runs on ST LMi - two in V and two in R. Flat fields were obtained from the dawn sky. I used 30 second exposures for ST LMi. The exposure time is something of a compromise; longer exposures would mean that a lower proportion of time would be lost reading out the CCD image (my readout time is about 15 seconds) and would also result in a lower proportion of readout noise in the images, but I would then run a greater risk of tracking errors ruining the images. With very faint objects one cannot afford to smear the image, and even with periodic error correction (see my last article in VSSC 103, page 8), my drive is not perfect.

After years of doing PMT photometry, which involved repeatedly moving the telescope and writing down the results by hand, observing with the CCD was very pleasant - I could even go indoors and leave the system gathering data on its own! As I had expected, it was occasionally necessary to adjust the telescope tracking, to stop the stars of interest from drifting out of the field of view. An unanticipated, but significant, problem turned out to be time-keeping; the computer clock was dreadful, and could drift by a few minutes in one hour! I frequently noted down both the computer time and UTC (from an MSF clock) in my log book. Perhaps I can find a more satisfactory solution in due course.

Data Analysis

This has proven far more time consuming than the process of acquiring the data in the first place! Fortunately, I like writing my own software. Indeed, trying to squeeze as much information as possible out of the data is a good way to appreciate some of the subtleties of CCD image analysis, of which there seem to be quite a few. In the past, my CCD friends had told me of nights of data which were still waiting to be analysed weeks after data acquisition. After generating more than 1000 images over four nights, I now have a better appreciation of the reason why! It is quite possible that some improvements can still be made to the analysis. Very briefly, data analysis for the ST LMi runs proceeded essentially as follows:

First the raw data files were dark and flat-field corrected. Also at this stage, a simple star search algorithm was to used generate a list of the coordinates of the stars found in each image and write them to a file called STARS.LST. The average width of the star images in each image was also obtained, so that images with poor tracking could be rejected from further analysis. One frame with good tracking was then chosen to define the master coordinate system. Several bright, but not saturated, stars were chosen to act as fiducial stars in this image and their positions were measured. A program which incorporated a pattern-recognition algorithm then searched through STARS.LST and attempted to locate these fiducial stars in the other images, and so determine the image offsets with respect to the master coordinate system. Field rotation (which in principle might arise in long runs due to slight polar misalignment) has been ignored for the time being; judging by the deviations of the fiducial stars from their expected positions after allowing for the offset (around 0.1 pixel rms), this seems a satisfactory approximation. Next, accurate positions of the variable and comparison stars in the master coordinate system were obtained from stacked frames. The final positions that were used for photometry used almost all the available frames with good tracking. The positions of blank areas of sky were also determined from a stacked frame. For the faint stars, it was important that the positions used for photometry were determined from stacked frames, rather than determined individually in each frame. The latter method, i.e. positioning the aperture to yield maximum signal in each frame, would systematically over-estimate the brightness of the star, since the sky noise is a significant fraction of the star signal.

For the photometry, I used a soft aperture, i.e. an imaginary circular aperture was placed at the expected position of the star and the pixels were weighted according to the fraction that was within the aperture. (Here I ignore the fact that the pixels are not quite square; they are slightly elongated E-W, but then the star image probably is too, due to imperfect tracking). For faint stars, the choice of the aperture size was important; too small, and one would not sample enough photons from the star; too large and one would sample too many photons from the sky. I examined the scatter in the results of photometry on a field star (GSC 1978 1314) which was of similar brightness to the variable, as a function of aperture size. I ended up using an aperture 4 pixels in diameter. As I expected, the best signal to noise ratio is obtained when the aperture diameter is about the same as the full width at half maximum of the star image.

The results are shown in the figures (which are plotted at the same scale to facilitate comparison). I have used a linear scale, since a logarithmic scale is inappropriate when dealing with signals with poor signal to noise ratio (it would exaggerate the low intensity part of the light curve and the noise). I have normalised the brightness to that of SAO 81659. Fortuitously, the field also includes the bright star 51 LMi, for which SIMBAD gives a Johnson V-magnitude of 7.63. I acquired some 3 second exposures to cross calibrate 51 LMi with SAO 81659; the latter turned out to have V=10.02 (consistent with its Tycho VT magnitude of 10.0). Use of other check stars in the field of view showed that SAO 81659 was constant to better than 1% between the pairs of nights. My derived magnitude of SAO 81659 should be pretty good, as it and 51 LMi have almost identical colour indices. For ST LMi, I've left the data in the instrumental system: there seems to be little point in worrying about the colour transformations, since the data are of low precision and the spectrum is unlike that of a standard star. Initial indications (from M67) are that my instrumental V-band is a fairly good match to the standard system, whilst my R band is shifted to slightly shorter wavelengths than the standard. No R-band data seem to be available for 51 LMi anyway.

I estimated the errors for these measurements, based on the measured readout noise of the CCD and the expected photon (shot) noise (the latter was calculated using the specified photoelectron/ADU conversion ratio). The error bars in the plots are 1 standard error, and they seem realistic (or, conversely, the scatter in the data is pretty much as expected). For example, on 25-26 March, 218 measurements of GSC 1978 1314 yielded a mean signal (relative to SAO 81659) of 0.0087 with an rms scatter of 0.0011; the computed error averages 0.0012. Hardly precision photometry, but probably acceptable for 30 second exposures of a 15.2 magnitude star through a colour filter with an 8-inch telescope !




Results

The reader may be beginning to wonder if, after all this effort on such a faint star, the data show anything interesting! Fortunately, the answer is 'Yes!'. First a bit about ST LMi: this system is a polar, consisting of a magnetic white dwarf which accretes material from a red dwarf. The magnetic field prevents the formation of an accretion disc, and an accretion column forms instead: material flows along the field lines towards a magnetic pole of the white dwarf. Here it is shock heated and cyclotron radiation is produced. This radiation is polarised (hence the name polar) and is also very red. In ST LMi, the stars do not eclipse each other, but the system appears bright when the cyclotron radiation-emitting region is visible, and fainter when it is hidden by the limb of the white dwarf. Cyclotron radiation dominates, and the system is reddest, during the bright phase. Early studies of this star attributed the faint phase optical radiation largely to the white dwarf (yielding V approx 17). However, more recently, Ciardi et al (PASP, 110, p1007) observed ST LMi in an extreme low state, when - as judged by the absence of emission lines - accretion had apparently stopped completely. It was then about V=18. (These notes are based mainly on a paper on ST LMi by J Bailey et al, MNRAS, 215, p179 (1985)).

It is very pleasing that many of these features of the system are present in my data. The bright/faint phase nature of the light curve is very apparent. The amplitude is generally greater in the red, as is expected. Night to night variability is also apparent, especially during the bright phase. Previous observers also commented on bright phase variation; this presumably represents a varying accretion rates onto the white dwarf. There also seems to be some smaller variations during the faint phase: perhaps this is due to variable emission from the accretion column well above the white dwarf. In this regard, I note that my V band observations always showed the system to be well above its low-state value of V=18, referred to above (note that 0.01 in my figures corresponds to V=15.0).

Acknowledgements I am very happy to acknowledge the loan of the BAA filter box. Also, as usual, this note has benefited from interrogation of the SIMBAD database.