British Astronomical Association - Computing Section - britastro.org/computing

Main menu

• Home
 
• History
 
• Handbook
 
• Data
 
• Charts
 
• Programs
 
• Morsels
 
• Links
 

This script provides the details of orbits of the planets (eccentricity, ascending nodes, argument of perihelion, etc.) at a given date. See the explanation below. It could be used for low precision calculations of the location of the planets, but is not suitable for high precision calculations (such as conjunctions or occultations) since pertubations are not taken into account. It will be reasonably accurate for recent historical dates or dates in the near future, but should not be relied on for dates in the far future or distant past. The number of digits given above should not be interpreted as an indication of accuracy.

In the table:
L is the mean longitude of the planet (degrees);
a is the semimajor axis of the orbit (au);
e is the eccentricity of the orbit;
i is the inclination to the plane of the ecliptic (degrees);
Ω is the longitude of the ascending node (degrees);
ϖ is the longitude of the perihelion (degrees).
See the diagram below for more details.

Note that for Earth the inclination is 0 and thus the value for the longitude of the ascending node has no meaning (set to 0.0)."

The algorithm is from Jean Meeus Astronomical Algorithms (2nd ed) Chapter 31 and is based on JL Simon et al (1994) "Numerical expresssions for precession formulae and mean elements for the Moon and Planets", Astronomy and Astrophysics 282 pp663-683. It was coded by Richard Kaye

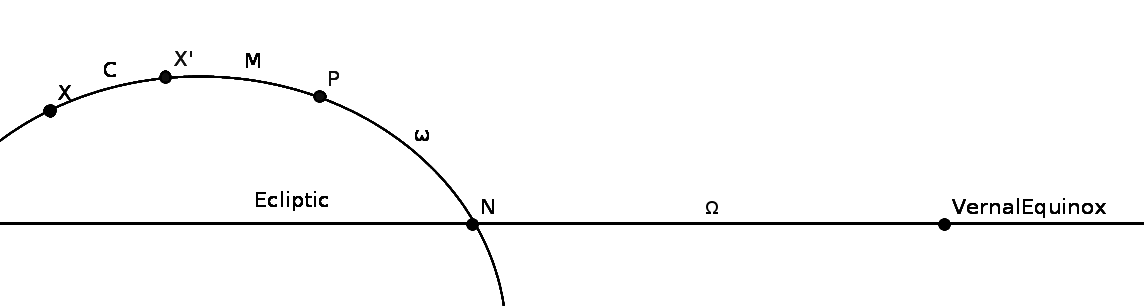
The diagram above shows the orbit of a planet as seen from the sun. The points and angles in the table and diagram are as follows. (All angles are as subtended at the sun.)

• The horizontal line represents the ecliptic and the curved line the orbit of a planet. The curved orbit is an ellipse of eccentricity e with the sun at one focus. This ellipse is in a plane at inclination i to the ecliptic and has semimajor axis of length a.
• The Vernal Equinox or First Point of Aries will be denoted ♈ and is shown to the right.
• The point N is the ascending node, the right-hand point where the orbit and the ecliptic meet, and Ω is the angle ♈N.
• The point P is the perihelion of the orbit and the angle ω or NP is the argument of the perihelion. The value ϖ is Ω + ω, the longitude of the perihelion.
• The point X' is the position of the mean planet, the angle M = PX' is the mean anomaly, The angle L in the table is Ω + ω + M, the mean longitude
• The point X is the true position of the planet, and the angle C = X'X is the equation of the centre, given approximately as 2e sin(M). The angle ν = M + C is the true anomaly and the quantity Ω + ω + ν is the true longitude of the planet.