ζ Herculis: a case study in the magnitude differences

2022 August 7

Christopher Taylor

Two slightly novel methods of visual observation in small telescopes of close, very unequal double stars are presented here and applied to the famous binary ζ Herculis with interesting, and possibly controversial, results. The comparison with the travails often experienced by professional astronomers observing this system with far larger instruments is highly instructive of the possibilities of ‘small-telescope astronomy’. The writer strongly urges other BAA members equipped with similarly modest instrumentation to ‘have a go’ at this fascinating and challenging binary.

Resolving ζ Herculis & the relative brightness of its components

The famous binary star ζ (zeta) Herculis (Σ 2084) is currently approaching widest separation (1.53 arcseconds or so, due 2024–’26; see Figure 1) in its 34½-year orbit – the same position at which it was discovered by William Herschel in 1782 July. Even compared with other 1–1½-arcsecond pairs, this is a difficult double around a large part of its orbit due to the great inequality in brightness of its two components. Night after night for many years the writer has been trying unsuccessfully, with both a 12½-inch reflector and a 4-inch refractor, to see the little companion star which Herschel, without any prior information or expectation, discovered with a 6.2-inch speculum-metal reflector well over 200 years ago – a humbling experience for a long-standing double-star observer who specialises in close, difficult binaries. Unsuccessfully, that is, until autumn of 2019 when the 4-inch gave the first glimpse and, conclusively, crosswire estimates of position angle a year later, which were closely confirmed afterwards by the ephemeris given in the BAA Handbook (neither that, nor any other source of the ‘expected’ value, having of course been consulted in the previous 12 months).

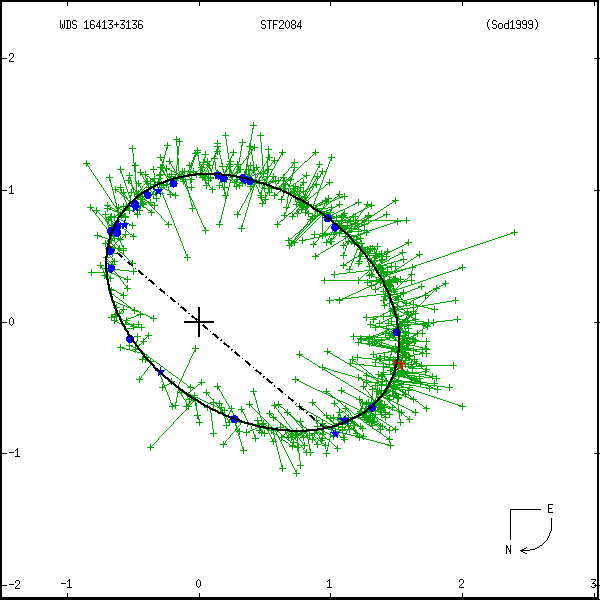
Those repeated failures with two instruments – both of which have on many occasions easily resolved more equal binaries at well below this angular separation, as well as slightly wider doubles having large, well-determined inequalities between the two components (the Δmag) – have long made this observer deeply sceptical of the surprisingly small Δmag = 2.5 listed for ζ Her in standard references (see Figure 2).¹ Having completed 2020’s convincingly positive observations, the writer now has quite definite observational evidence on the issue, which appears to disagree with that quoted figure by a considerable margin and thus makes perfect sense of the earlier failures. This raises interesting issues of wider relevance in double-star astronomy and is the main point of the present paper.

The role of the brighter star’s diffraction rings

In a small telescope, the observational case of ζ Her and all comparable close, unequal doubles hinges entirely on the diffraction rings of the primary star’s Airy pattern. Small refractors consistently produce much clearer views of the diffraction rings of bright stars than do larger reflectors,² but even they often show the rings as broken into short arcs, or visible only on one side of the star-disc, and that even in excellent seeing when both instruments define the Airy disc perfectly. The evenness of the rings’ illumination is, in fact, hypersensitive to the slightest optical disturbance, atmospheric or instrumental, at a level well below the limit at which that begins to distort the shape of either disc or rings at all.³ In the writer’s experience, the ring fragmentation seems to be an atmospheric ‘seeing’ effect, while the lopsidedness appears to be due to temporary coma at the 0.1–0.2λ level, possibly induced by uneven cooling of the telescope’s objective. Both effects vary widely from night to night, even when the seeing is good enough to see the rings at all.
It is, of course, a commonplace of double-star astronomy that the primary’s diffraction rings are a great nuisance in cases like this, where a faint companion lies at just that distance which puts it right on the first ring produced by the telescope used,⁴ so rendering the small star practically invisible. That is one major factor in making the resolution of close doubles having Δmag > 2 far more difficult than that of equal pairs at the same separation. The autumn 2019 and 2020 observations of ζ Her with the 4-inch refractor have, to the contrary, stood this situation on its head completely by turning those travails to positive advantage: rings, arcs, coma and all.

Turning the behaviour of the rings to advantage

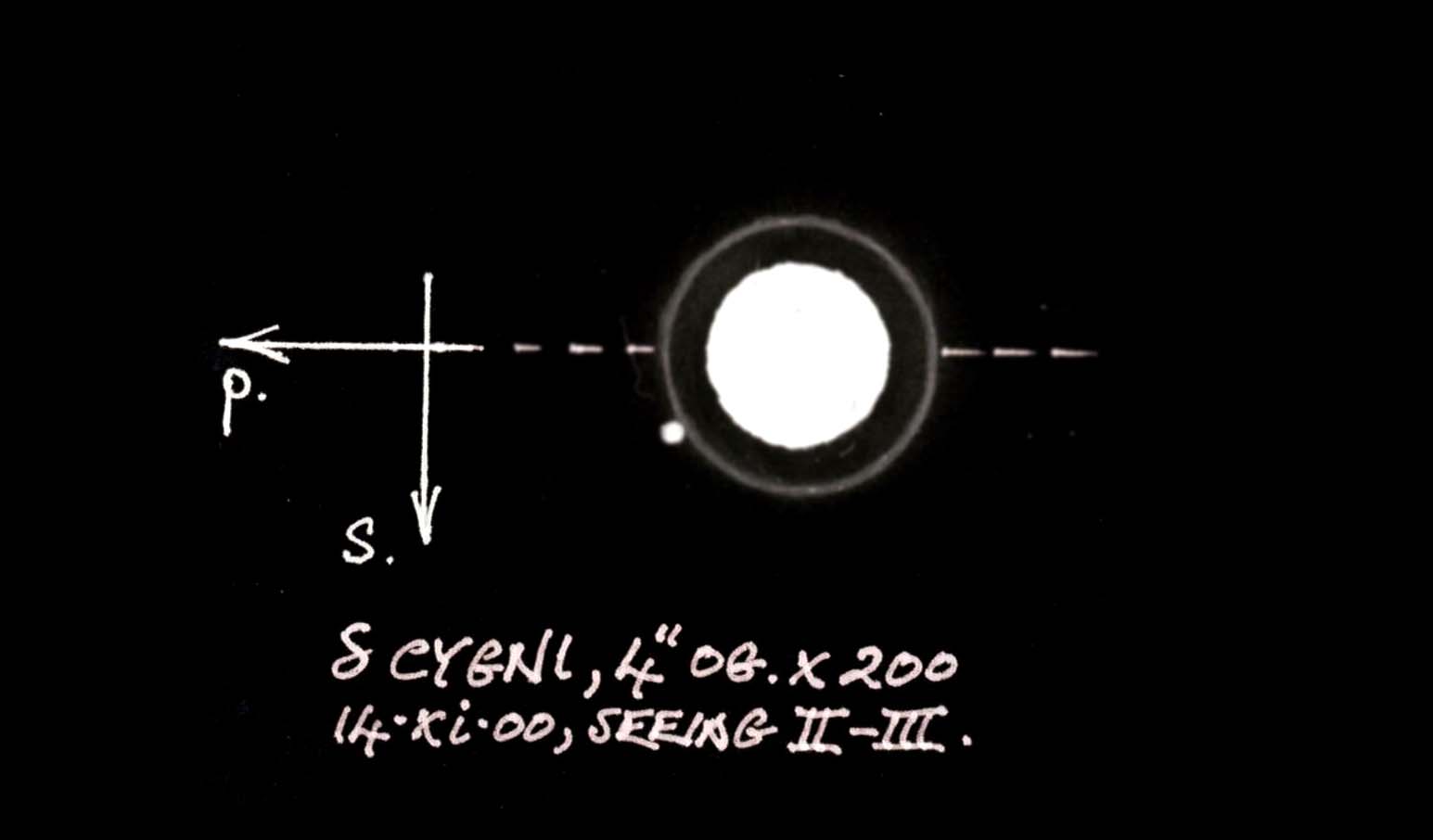
First consider the 180° lopsidedness, caused by coma, in the light distribution of the primary’s first ring. Computer simulations show that a very small amount of coma of order λ/5 or less is sufficient to drain all the illumination in the first ring of the Airy pattern round to one side.⁵ This leaves the opposite side right up to the edge of the central disc completely dark, without causing the slightest geometrical distortion of either disc or rings – that is, the effect is purely one of tangential or azimuthal redistribution of light in the undistorted diffraction image: see Figure 3. This is precisely what is quite often (but not always) observed with the 4-inch refractor on nights of good definition.

The possible strategy this offers for very significant improvement in the visibility of close, faint companion stars was discovered by the writer quite by accident on just such a night in 2017 May, when he was unexpectedly granted an exquisite view of ι (iota) Leonis (Σ 1536, missed by Herschel and discovered by Struve in 1827). The effect just happened on that occasion to drain all the light of the primary’s rings clear of the tiny companion star, leaving it plainly visible on a dark ground (see Figure 4).⁶ In the autumn 2019 and 2020 observations of ζ Her with the 4-inch, this was quite deliberately put to good use, by turning the telescope tube in its cradle to place the lopsided ring arcs in the quadrant away from that in which the companion star was known to lie ( the only prior information known to the observer at the time). Even with such assistance and extremely good seeing, this particular double is a very tough target in this aperture, but the companion was nevertheless seen repeatedly as a minute needlepoint of light just clear of the edge of the big star’s disc – a very beautiful sight, if evanescent.

Secondly, having used that trick to enhance the visibility of the companion star, the primary star’s rings become a positive advantage in providing a calibrated image scale, allowing quite close estimation of the two stars’ separation. In difficult cases where the companion lies anywhere from the primary’s first dark space to its second diffraction ring, this is useful in then providing one objective criterion for subsequent verification of the observation by comparison with authoritative published data (the other such criterion being the position angle).

Finally, and most relevant for the purposes of this paper, is the fragmentation of those rings into short arcs, especially the primary star’s first (and therefore brightest) ring, in cases such as that of ζ Her currently observed with the 4-inch aperture. In these cases, the companion and the ring arcs lie at much the same distance from the primary,⁷ and the arcs therefore provide legitimate ‘comparison stars’ for visual estimation of the stellar magnitude of the companion relative to the primary. Standard diffraction theory gives precise values for the proportions of the total light sent into the central disc and each ring, in stellar images produced by a well-corrected objective (which the 4-inch refractor is). Of course, we have no immediate way of estimating closely how much of the light of, for instance, the complete first ring is present in any one of those arcs into which it is often broken, but given that there are always at least two or three arcs of comparable brightness, it is clearly never more than about 40–50% in extremis. This, combined with the diffraction theory results, therefore provides an objectively calibrated upper limit on the brightness of the ring arcs, so that their visual comparison with the faint companion star provides a secure lower bound on the double’s Δmag. As a simple, and admittedly crude, visual photometric method we can do no better and it is sufficient for present purposes.⁸

The classical diffraction theory of the Airy pattern requires 7% of the total light in a telescopic star image to go into the first ring, which is 8.4% of that in the central disc, in an optical system free of significant spherical aberration.^9,10

(Login or click above to view the full illustrated article in PDF format)