BAA comet observations: magnitude parameters

2023 June 7

Jonathan Shanklin

BAA observations of comets have been analysed in a similar way since 1990, with results published in the annual series ‘The brighter comets of …’. With over 25 years of one-off cometary appearances and returning periodic comets, some conclusions are possible. In this paper, statistics on the distribution of magnitude parameters of comets and the different types of behaviour of multiple-return periodic comets are presented.

Introduction

Each observer is different, and indeed with two eyes even one observer can see things differently depending on which eye is used. From my own experience, one eye sees more blue and the other more yellow, which gives a different colour perception depending on which eye is used, with the dominant eye providing the strongest signal. It is therefore to be expected that individual observers will exhibit systematic differences from the mean (biases) and this was explored in one of the earliest papers in the series. If there are many observers for a comet, these biases will cancel out, but if a comet is observed by only a few observers and at different parts of the orbit, this could affect the computed light curve.

In addition to observer biases, differences can be introduced by the instrument, with short-focus reflectors using a low magnification giving brighter magnitudes than long-focus refractors using higher magnification. Observing conditions also play a part, particularly with diffuse comets exhibiting a large outer coma which is obliterated by any light pollution. Low comet elevation or twilight conditions will also obscure the coma, leading to fainter estimates.

Some of these effects should not apply to visual equivalent magnitudes (VEM) obtained using electronic detectors. It is however clear that comets with a large coma diameter are usually reported as having a fainter VEM than that seen by visual observers.

Bias corrections, both for observer and instrument effects, can be computed when there is a really well observed comet. Such objects are unfortunately few and far between, with the last to have over 1,000 observations being 2014 Q2 (Lovejoy). For that comet, there was only one observer reporting a significant number of VEM magnitudes. 2017 T2 (PanSTARRS), which reached perihelion in 2020, was less well observed with just over 500 observations, but several observers reported VEM magnitudes for it. Considering those observers who made more than 10 observations of this comet, the mean bias correction for all but one observer was less than 0.5 magnitudes. That particular contributor, who observes from a good location and has very sensitive eyesight, almost always reports brighter than the mean.

The standard deviation of the observations contributing to each bias is however higher for the VEM magnitudes than for the visual magnitudes. The bias standard deviation is slightly reduced when a correction for reported coma diameter is also applied. This confirms that the amount of coma that is recorded is a significant factor in how bright a comet appears.

Magnitude parameters

There are two basic ways of describing the evolution of a comet’s brightness. For most comets, the key parameters are the distance from the Sun and the distance from Earth. The brightness changes caused by the changing Earth distance (Δ) follows a standard inverse square law. The changing distance from the Sun (r) can have a similar to much greater effect and varies from comet to comet depending on how its activity evolves. The comet will also have an intrinsic or absolute magnitude (H), which is how bright it would be if it was exactly 1au from both Earth and the Sun. This gives an equation:

m = H + 5 log (Δ) + k log (r)

For many comets there are not enough observations to determine k reliably, so a value of 10 is often assumed, giving an absolute magnitude that is called H₁₀. Some periodic comets brighten more rapidly than this, in which case a value of 15 (H₁₅) or 20 (H₂₀) is assumed when assessing variation in absolute magnitude. If H or H₁₀ is small, the comet is intrinsically bright. Very few comets have negative absolute magnitudes, but C/1995 O1 (Hale–Bopp) was an exception with an H value of –0.7, mostly because it had a large nucleus of roughly 60km in diameter.

A large value of the absolute magnitude implies a small-sized or weakly active nucleus. For example, 124P/Mrkos has an H value of 14. If k is small, the comet brightens slowly, and a value of less than 5 suggests that activity is being choked off as the comet approaches the Sun. If k is large then the comet brightens rapidly, though few comets have well-determined values larger than 25.

A few comets show a slightly different pattern of behaviour, where it is the time (t) from perihelion (T) that influences activity, giving the equation:

m = H + 5 log (Δ) + k (T – t – dt)

with the activity often being greatest some days or weeks (dt) after perihelion.

Since the first paper, H₁₀ values for nearly 900 comets have been computed, along with H and k values for just over 300. Around 60 comets show the linear pattern of behaviour, of which 40 are periodic.

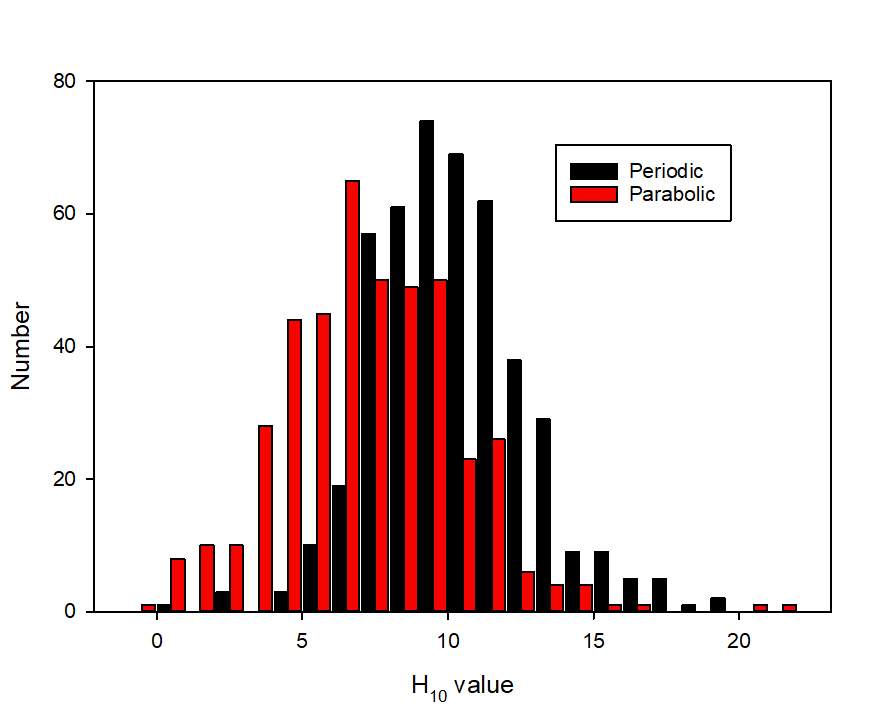
Absolute magnitude

The distribution of the H₁₀ values is roughly a normal one, i.e., having most values close to the mean with a steadily smaller number the further from the mean you get. There is however a clear difference between the mean for parabolic comets and that for periodic comets. In part this may be an observational bias, since there are many opportunities to observe periodic comets and whilst they may be missed at an unfavourable return, they may be discovered at the next favourable one. In contrast, there is only one chance for a parabolic comet to be observed, so they are generally only seen if they are intrinsically bright or have a favourable return.

Another way of looking at the H₁₀ values is in terms of the perihelion distance. This shows that in general (as might be expected) a comet has to be intrinsically brighter in order to be seen if it has a larger perihelion distance. When comets get very close to the Sun, they may become visible due to the intense solar radiation, despite having an intrinsically faint absolute magnitude. There is an apparent upper limit to the H₁₀ value for a given perihelion distance, particularly at smaller values of q. This may imply that there is a minimum nuclear size that can survive to show cometary activity. As an example, at q = 2au, the maximum H₁₀ is around 14, which for a perihelic opposition would imply a total magnitude of about 17: well within range of the more recent VEM measurements.

Because there are fewer comets showing a linear brightening behaviour, the numbers are too small to discriminate between parabolic and periodic comets, but together they show a similar distribution.

Several authors (e.g. Hughes (2002),¹ Sosa & Fernández (2011)²) have explored the relationship between absolute magnitude and nuclear size. The latter suggest:

log (r) = 0.9 – 0.13 H₁₀

Other authors give a broadly similar equation and the application to selected comets is discussed later in this paper.

(Log in to view the full illustrated article in PDF format)