British Astronomical Association

Supporting amateur astronomers since 1890

Using a lunar eclipse to measure the diameter of the Earth’s shadow

2021 October 3

Mark Lonsdale, Stephanie Hudson, Haocheng Lu & Geoff McNamara

Lunar eclipses are often occasions for amateurs to take spectacular images of the red Moon. During a recent lunar eclipse in Australia (2021 May 26), however, we tried also to do some basic science. With imaging and simple geometry, we measured the diameter of the Earth’s shadow (the umbra) as the Moon passed through it. Although the dimensions of the Earth’s umbra are known, the exercise was an opportunity for learning about astronomical geometry that connected us to the ancient astronomer Hipparchus, who used a lunar eclipse to determine the radius of the Moon. We modified a published study (Jiménez et al., 2014) to measure the Earth’s shadow using two methods.

Method I

This involved measuring the transit time for the umbra across a fixed point – the crater Tycho – on the lunar surface. In the previous study,1 this was done using a video feed and subjective estimation of the entry and departure of the shadow across a wide field of view. We modified this by quantifying the gain value in a video feed of Tycho (Figure 1), at one-minute intervals, to produce a light curve. We set the ‘auto-histogram’ in our capture software (FireCapture) to hold at 60%. The software then adjusted the gain to maintain 60%, as the light faded and brightened with the passing of the umbra. We simply recorded the resulting gain value to provide the light curve (Figure 2).

Figure 1. The Tycho field, during the lunar eclipse of 2021 May 26. To acquire and process these images, we used FireCapture software, a guided Orion Optics UK 400mm ƒ/4 Newtonian, and a ZWO 224MC planetary imaging camera. We captured 60s videos, which we stacked in Autostakkert 3 and sharpened in Registax 6. The edge of the umbra advanced from the top left and fully covered the field by 10.09 UT, departing towards the bottom right at around 12.24 and leaving the field in penumbra again by 12.39.
Figure 1. The Tycho field, during the lunar eclipse of 2021 May 26. To acquire and process these images, we used FireCapture software, a guided Orion Optics UK 400mm ƒ/4 Newtonian, and a ZWO 224MC planetary imaging camera. We captured 60s videos, which we stacked in Autostakkert 3 and sharpened in Registax 6. The edge of the umbra advanced from the top left and fully covered the field by 10.09 UT, departing towards the bottom right at around 12.24 and leaving the field in penumbra again by 12.39.

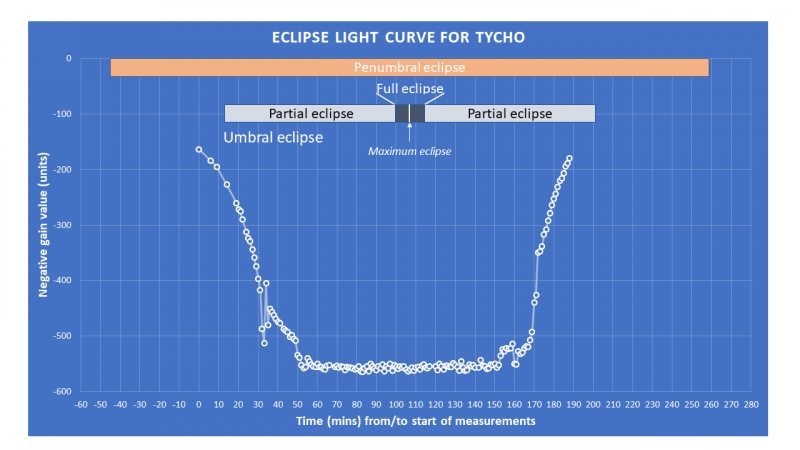
Figure 2. Method I – a light curve was obtained as the edge of the umbra passed across the Tycho field. The field was already in the penumbra by the time we started taking readings. The light level is expressed as the gain required to maintain a histogram of 60% in FireCapture. We multiplied gain by –1 to give a more intuitive downturn in light as the shadow passed across the field.
Figure 2. Method I – a light curve was obtained as the edge of the umbra passed across the Tycho field. The field was already in the penumbra by the time we started taking readings. The light level is expressed as the gain required to maintain a histogram of 60% in FireCapture. We multiplied gain by –1 to give a more intuitive downturn in light as the shadow passed across the field.

From the edges of this curve, we measured the duration of the passage of the shadow. Knowing the speed of the Moon in its orbit (1.022km/s), we came up with a diameter for the umbra of 9,750km. Note that Tycho did not pass across the full diameter of the Earth’s shadow, but through a chord, and a correction for the distance of Tycho from the centre of the Earth’s shadow gives a diameter for the umbra of 10,034km. The shadow is cone-shaped, so the exact diameter of the cone depends on the distance of the Moon during the eclipse, but the value compares well with that found by Jiménez et al. (2014), at 9,944km.

Method II

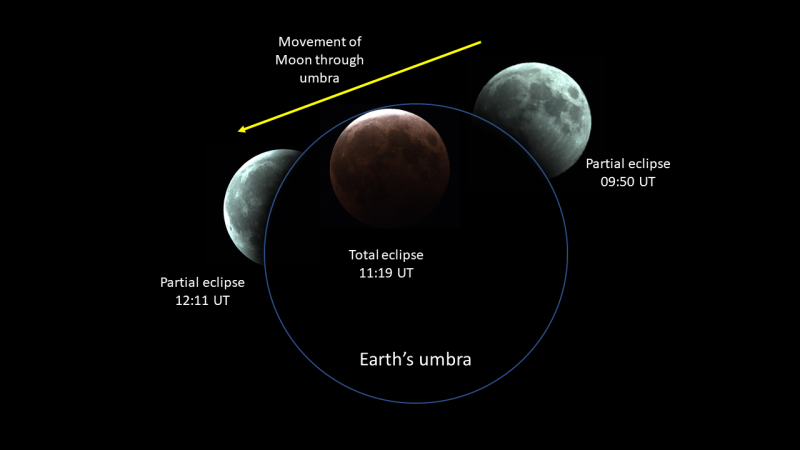
The second method was related to Hipparchus’ estimation for the radius of the Moon (see again Jiménez et al., 2014). Here we captured images of the whole Moon as it entered and left the Earth’s umbra. We then drew tangents to the edge of the umbra to estimate its radius (Figure 3). This more subjective approach gave us an estimated umbra diameter of 8,800km (with a range from 8,030–9,651km) – about 10% less than for Method I, but not bad considering the greater subjectivity involved.

Figure 3. Three images captured during the eclipse using a 100mm ƒ/5.8 SharpStar refractor, ×0.8 focal reducer and ZWO 294MC camera, with the Moon superimposed on a presumed outline of the Earth’s umbra. Note that the camera’s gain was increased during totality to capture the red tinge of the eclipsed Moon.
Figure 3. Three images captured during the eclipse using a 100mm ƒ/5.8 SharpStar refractor, ×0.8 focal reducer and ZWO 294MC camera, with the Moon superimposed on a presumed outline of the Earth’s umbra. Note that the camera’s gain was increased during totality to capture the red tinge of the eclipsed Moon.

Figure 4. Method II – we chose two images of the whole Moon (see Figure 3), at entry and egress from the umbra, and drew tangents to the edge of the Earth’s shadow, by eye. This allowed us to calculate estimates (r1 and r2) of the radius of the shadow for the two images, by measuring the points of intersection of the perpendiculars to the tangents (see Jiménez et al. 2014).
Figure 4. Method II – we chose two images of the whole Moon (see Figure 3), at entry and egress from the umbra, and drew tangents to the edge of the Earth’s shadow, by eye. This allowed us to calculate estimates (r1 and r2) of the radius of the shadow for the two images, by measuring the points of intersection of the perpendiculars to the tangents (see Jiménez et al. 2014).

You are welcome to contact us for more details (see p.321 of the October Journal for an e-mail address) if you would like to repeat the work during the upcoming lunar eclipses (2021 November and 2022 May).

Mark Lonsdale, Stephanie Hudson, Haocheng Lu & Geoff McNamara, McNamara-Saunders Astronomical Teaching Telescope (MSATT), Canberra, Australia

References

1   Jiménez M. A. P. et al., ‘Measuring the size of the shadow of the Earth’, Gloria Project DEL-089 (2014): bit.ly/2YQ9gir (accessed 2021 August)

The British Astronomical Association supports amateur astronomers around the UK and the rest of the world. Find out more about the BAA or join us.