› Forums › Meteors › More meteor spectroscopy › Hi Gents,
Hi Gents,
Thanks for the comments. It’s great to hear alternative perspectives and different experiences!
Robin, do you mean this….
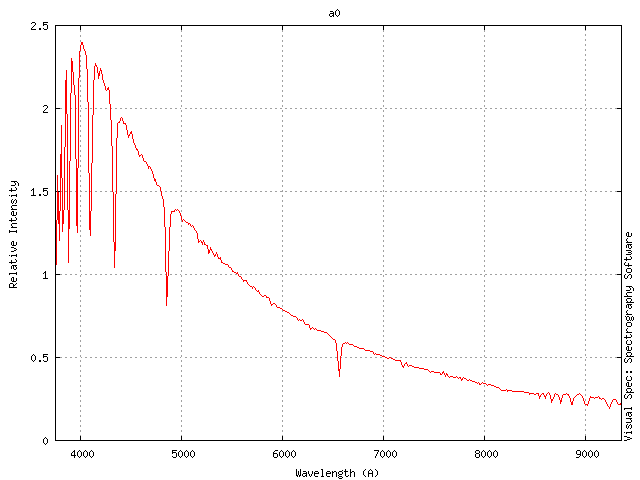
Perhaps not worded too cleverly on my part. The “oscillations” being the converging H lines. However using this method on meteors is not quite the same as using it on stars. For example when you divide a meteor spectrum through by a stellar spectrum there is still the issue of where exactly to select points to derive a continuum to act as the response.
I tended to end up with curves that were rather wavy. Below is an a quick plot I’ve made using an actual repsonse from an early test. Maybe its the methodology (as you describe in the examples on your web site) but for meteor spectrum correction I just don’t think it’s quite right.
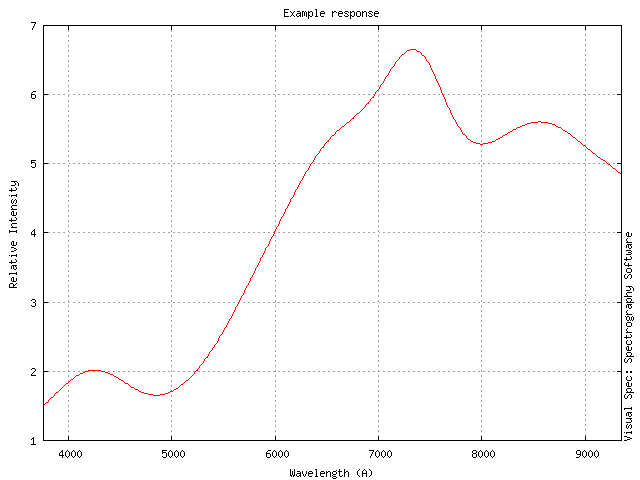
If one uses ones imagination it approximates the nominal silicon photodiode curve as it surely must. (Unless there is evidence that a silicon based detector was not used in the visible of course). Thats what put it into my mind to invesitgate further.
Here is a nominal silicon photodiode response curve I produced from date taken from a large photodiode manufacturers website.
![]()
Dividing thorugh by this will give a form to the meteor spectrum then the other calibrations and corrections can be done as you discuss. However the problem with this approach is that although the form of the curve remains the same the peak moves slightly depending on how each photodiode site is biased by the electronics. THAT is a dark secret known only to the manufacturer!
From my experience at work I’d say the peak was closer to 820-850nm in real photodoides but I think that can be corrected itself by the appropriate normalisation point before division.
But then again maybe we’re right back to where we started…. It’s great fun!
There are a couple of papers by the various experts such as Borovicka and Jenniskens deriving absolute fluxes which is what we’d like. They seem to rely on various measurements made on the ratio of particular groups of lines (such iron lines in the blue) to derive an effective temperature. I’m not sure I understand the maths behind it but in some cases, but as promoted by Borovicka, there are different temperature regimes that complicate the matter further. These temperatures are generated by the particular properties of the meteoroid and its encounter with Earth, size, composition, velocity angle of entry etc. So getting what would be in effect an inverse black body curve for the appropriate physical temperature to do further calibration with is very difficult because we don’t know this in advance!
It is rather ironic that the very atmosphere that generates the meteor itself scatters efficiently in the blue. Right where the interesting lines are that we need to measure in the first place. Who’s say Pacha Mama doesn’t have a sense of humour….
I’m beginning to think “tricky” just doesn’t cover it ;-).
cheers,
Bill.
