Forum Replies Created
-
Posts
-
Hi again Steve,
I completely agree with you with what you said about the errors. The bit I meant to calculate was the error on the estimate of the obscuration and magnitude. If we take your +/- 1 pixel example, the largest value of the angle subtended by the chord w is derived from the ratio 847/1199 which corresponds to w=1.568860462 radians. The smallest angle is derived from the ratio 845/1201 which corresponds to w=1.56084678 radians. So the upper and lower limits to the obscuration percentage are 18.11% and 17.85% respectively, which roughly means that your observed value is 17.98 +/- 0.13 (compared to the predicted value of 17.96%). With respect to the magnitude the upper and lower limits are 0.2922 and 0.2894 respectively, which means that your observed value is 0.2908 +/- 0.0014 (compared to the predicted value of 0.2910). So it seems we would have to work a bit harder in accuracy before we could start to determine if the observed value really differs from the prediction (and this is what would be of interest).
Duncan.
Hi Steve.
Wow, that’s great. It is nice to see that you could get a measurement for the magnitude and the obscuration which so nicely agrees with the prediction. Very satisfying. As regards my formula I am pleased that you could verify it. I too slogged through some trig but I spotted this simplified form of it at the end. I must work out what roughly the errors would be on these values given that you could measure things to within a pixel or two. I haven’t actually checked the assumption that the moon and the sun were approximately the same apparent diameter for this particular eclipse. Oh, actually, on that diagram of the eclipse in the handbook it has the apparent semi-diameters of the sun and moon at greatest eclipse (S.D.=…). Taking these to be the numbers we need it would imply that the moon was slightly smaller than the sun?
Thanks also for explaining about the eclipse diagrams in the handbook. Yes, that link you gave to that NASA page does definitely help! I will keep a note of it.
I also liked your two videos of the eclipse, especially the second one which shows that the path of the eclipse is a straight line. Very clever.
Duncan.
Hi Alex. Thanks very much for replying to my query. All very interesting.
I must admit that I understood eclipse obscuration (or percentage coverage) better than I did magnitude as you do tend to see predictions for these more in articles in a run up to a partial eclipse. I did look at the BAA handbook and the observer’s challenge beforehand. One thing I could point out as a relative newcomer to all this is that I didn’t understand what the blue line predictions were in the handbook as there didn’t seem to be a key (that I could see, unless perhaps, someone could point me to where it is)! I see now the numbers on the blue lines are probably magnitudes rather than maximum obscuration (I have just learnt something new in that magnitudes are quoted for maximum coverage). On the next page, though, the numbers are given as max obscuration (so even the handbook can’t decide what to display!). However, I do agree with you that magnitudes may be better because they are linear rather than depending on area. I must say that quite a lot of the other numbers quoted on page 13 of the 2022 handbook don’t mean much to me.
I think that what trying to measure the percentage obscuration did for me was to really make me understand what these terms meant and the bit of maths required to calculate the area of intersection of two identical circles was enlightening (no one has yet told me whether what I quoted was right or wrong yet!). Clearly it is more complicated if the sun and the moon are not the same apparent diameter but the same rules apply.
I guess what I am trying to say, perhaps, is that even though the mechanics of the earth moon system is very well known and calculating magnitudes or obscurations from our observations is not going to improve that knowledge, for those of us on the learning curve it is still very instructive!
Thanks for the link to the article. I will have a read of this at some point.
Duncan.
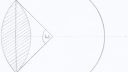
I am going to stick my neck out here but I wondered if observers actually calculate the obscuration of the sun by the moon from the pictures that they take of the partial eclipse or does this have no value because the earth/moon system dynamics is so well known? I think that the obscuration percentage is given by the simple formula 100(w – sin w)/pi if you assume that the sun and moon appear to be the same anglular size. If you draw a chord between the points where the moon’s shadow touches the sun’s edge (the chord PP’ in the attached diagram) the angle w (in radians) is the angle subtended by P and P’ from the centre of the sun’s image. If you have an image of the partial eclipse you can measure (in pixels) the diameter of the sun’s disc and the length of the chord l and then w = 2 arcsin (l/d).
For example, for my image of the partial eclipse taken at 09:45 UT on the 25th from 52 degrees 44 minutes north and 1 degree 28 minutes east, l was 209 pixels, d was 311 pixels and so the obscuration was about 15% at this time (this was about 15 minutes from maximum coverage).
Even if the calculation has no scientific value, it may still be interesting to calculate and compare with prediction.
Attachments:
Thanks Gary. I hadn’t added myself to the BAAVSS alert group, so I have requested this now. Can the new chart 106.04 be used in the online database already?
Duncan.
Thanks Bill, that kind of makes sense that there is some kind of multiplying factor that is observer and instrumentation dependent. I was wondering how this all worked because I could see that the better the instrumentation and resolution you had, the more sunspots you might count. I haven’t tried using a Stonyhurst disc yet, that was something I was going to try and grapple with next. I think for the moment I will continue with my approach of projecting the image first and getting a handle on the basics before moving on to solar filters etc.
Thanks very much Peter, that clarifies things a lot. I hadn’t thought that it was the center of the groups that was used to determine their distance apart on the solar disk, I had just assumed that it was how close their edges were. So that helps. I also didn’t realise it was just the umbrae that counted towards the spot number, either. I think I might try and add some observations to the database that you mentioned once I get the hang of things a bit better but I notice from your newsletter that we can email images to you. Do you have any preference about whether the image is annotated in any way (e.g. with AR numbers?). I note using the time, date and initials in the file name and copying them to Lyn. Any preferred format for the file name? many thanks.
Another aspect of the light curve of this star that interested me was that from time-to-time the maxima appear to be double peaked. This has been shown nicely by some recent observations using CMOS detectors (see the attached file which has been produced from the BAA database). If you look at the light curve after the 1st Jan 2022 you can see (green data points) that Z UMa reached a maximum of about magnitude 6.6 around the 14th March, then it faded a bit to about 7.7 around the 21st April before brightening again to about magnitude 6.8 around the 22nd May (roughly 69 days from peak-to-peak). The same double peak is seen in the visual data (black circles) but the scatter in the CMOS data is much tighter. Looking back at the four maxima prior to this the visual data (black circles) hint that this double peaked behaviour has been been developing as time progresses.
If you go back further in time other reasonably clear examples of a double peak can be seen in August 2016, January 2008 to July 2009, January 1999, July 1999 and July 1995 (I haven’t gone back further than this). So what is causing this? One suggestion has been that this is due to the interaction of different pulsation cycles within the star but this is not so easy to understand if, as John Greaves says (see my first post), after 1995 there is virtually only one pulsation period of 189 days. With more people carrying out observations using more accurate electronic detectors it will be interesting to see how often this double peaked behaviour appears.
Attachments:
Thanks Jeremy for all these useful links. I have had a brief look at the T UMi paper and scanned the June edition of the AGB Newsletter. People who are modelling the evolution of stars on the AGB seem very keen that we keep monitoring stars whose periods are changing over time.
Hi Lyn, this is embarrassing. I forgot to subtract an hour from my timing of my solar image I took on the 21st April. So this should read 11:07 UT not 12:07 UT. Sorry about this.
Hi Lyn, I am a new member of the BAA and thought I would try and contribute to this thread (my first post on the forum). I took this image on the 21st April at 12:07 UT using a Celestron NexStar 102SLT. I used a 25mm eyepiece and a star diagonal to project the image onto white paper. I have rotated it as best I could to give the correct orientation. There are two versions of the same image. One has the sunspot groups annotated. I hope that this is useful to you.
